NEW DISCOVERY
Is ‘Euler’s Identity’ ((e^iπ)+1 = 0) really the “Most Beautiful Equation in Mathematics”?
It requires an Imaginary (-1^.5) and Complex plane of numbers…..but is e^π pointing to something even more simple and sophisticated at the same time? What if we perhaps replace i (Root-1) with the Fractal Root of -1? Talal and I wrote a white paper on Fractal Roots a couple years ago and you can find it here….
What’s a Fractal Root you say?
It’s two identical numbers separated by one ordinal (decimal) position. In this context: Fractal Root 1 = 3.16227766 and .316227766 (both numbers are actually irrationally identical). Their product is perfectly 1.00000. We believe the Universe uses this for Fractal ”management” across vast scaling from subatomic structures to galaxy clusters.
So what does it do to this Euler Identity Equation?
Well….(1/(e^iπ))+1 = 1/α…..ALPHA, as in the ‘Mysterious’ Fine Structure Constant?! α = .00729735 (and α^-1 = 137.036). Alpha is the threshold separation of Light and Darkness in Electron Coupling (Photon Reflection versus Photon Absorption). Wait, didn’t the world-renowned Physicist Richard Feynman say that no one has been able to find the equation for this, the most enigmatic of dimensionless constants?! (Swipe for Feynman.com commentary–by Feynman himself).
Can we derive a Geometric Proof for this?
Why yes, we can: (Swipe) Embedded in a circle and it’s Diameter….10^4/e^π = 432…..A circle with circumference 432 (431.99) has a Diameter of 137.5077….which is the exact value of the Golden Angle = A°; now, let’s subtract ((φ(360°))*10^-3)^2 from A° = α^-1 where Alpha is equal to .00729735…..an astounding 8 decimal digits of accuracy.
So, is Euler’s Identity pointing to something even more beautiful than the symmetry of two related irrational numbers being ‘plugged’ back to -1 through the rather ‘opaque’ (shall we say?) Imaginary Plane/Complex Numbers or rather might it be pointing us to the beauty and simple sophistication of the very nature of Light’s separation from Darkness?





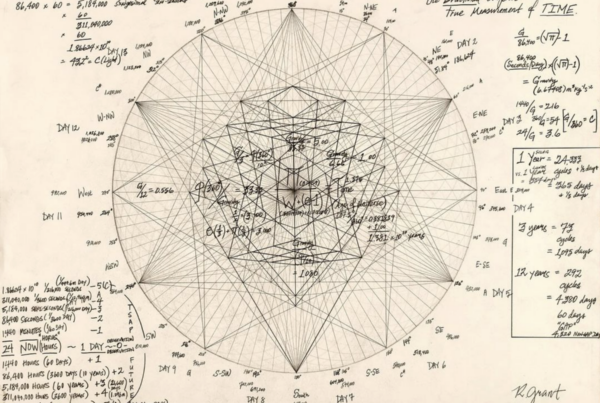
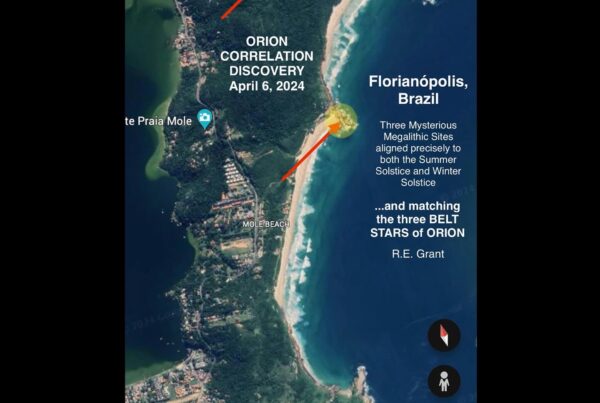
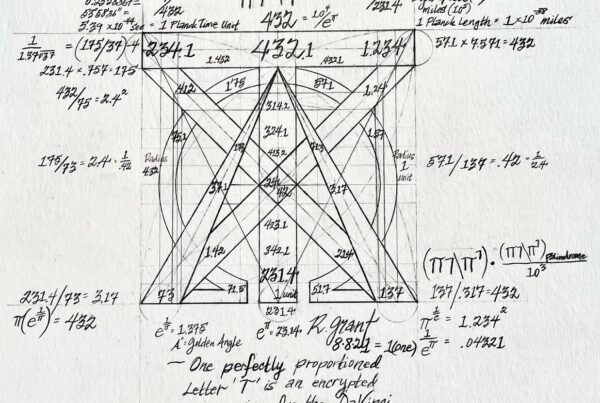

In my humble opinion it is the separation of dark matter … It´s to go beyond the limits of time and space in the infinite limit of the perimeter of the fractal