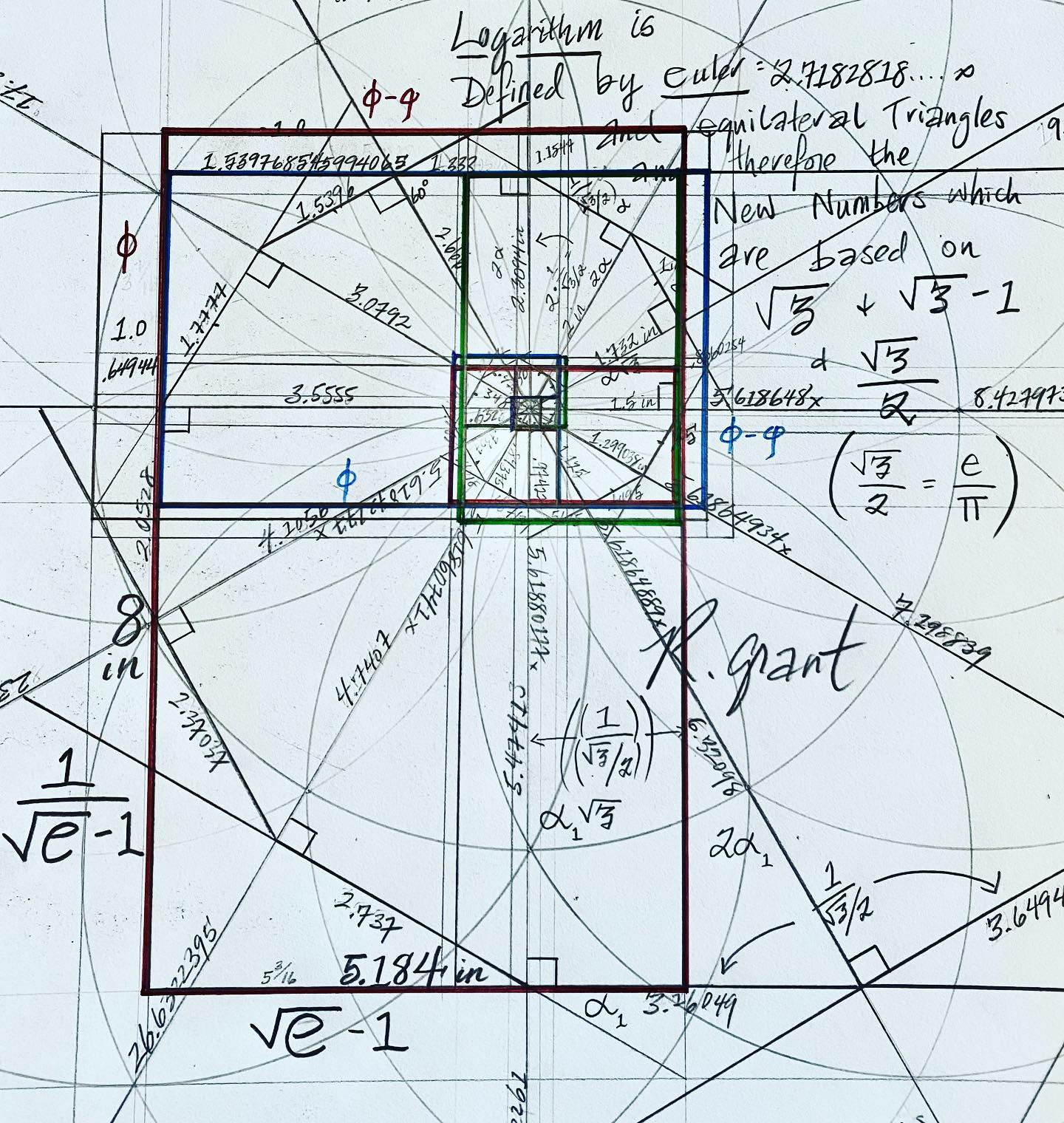
How Equilateral Triangles Make Φ…..through the Euler Number and the Natural Logarithm. It appears that Equilateral Triangles make Perfect Golden Ratios in the Euler based Logarithmic Spiral. Prior mathematical thinking was that the framing of a Phi Spiral would require side lengths of a rectangle to be φ and Φ-φ.
What I have just found is that the golden proportion emerges solely from Equilateral Triangles rotating in 12 positions expanding outward based on 1/(e^.5)-1 and (e^.5)-1…..and of course: e^x and the Riemann ζ ‘Zeta’ Function: (π^2)/6. Interesting also that I found that ζ^4 = (3^.5)-1 AND that the 16th Root of e = ((ζ-1)/10)+1. This may also explain why e-1(360°) = 618° (a degree value for φ)…